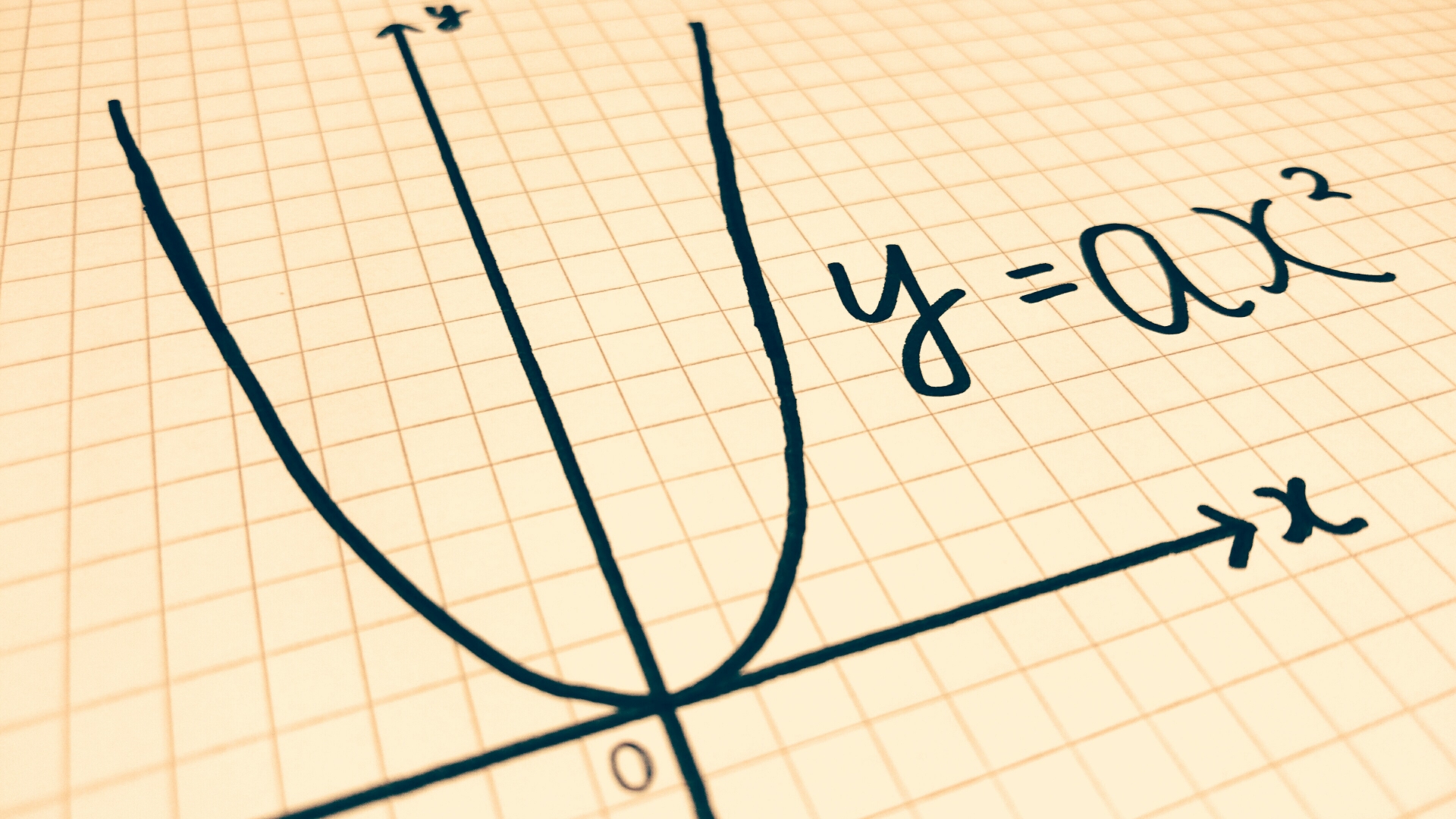
2023.10.10
元教員が岐阜県入試を分析!-関数-
どうも!
T’s(ティーズ)塾長の小川です!
公立小・中学校,附属学校教員として14年間勤務したのち,ひとりでも多くの算数・数学を苦手とする子ども達の役に立つために退職,独立,起業。
2021年から独自のオンライン教材開発を続けています。
自分自身の教育現場での経験を生かし(プロフィールはコチラ),
「新しい切り口の分析」や「効率のいい勉強方法」を提案していこうと思いますので,数学に悩みをもつ中学生や,その保護者の方は,このシリーズをうまく活用してほしいなぁと思っています。
元教員が岐阜県入試を分析!-小問集合 関数編-
さて,
前回の記事では,その前の記事にひき続き,岐阜県入試(数学)の小問集合の中でも,特に”方程式”の問題についてみてきました。
まだお読みでない方は,是非コチラの記事もあわせてお読みください▼▼
今回は,小問集合に出題されている
”関数”領域
の問題に絞って確認していってみましょう。

小問集合で頻出の関数領域も近年では・・・
学校教員の頃,
「関数が苦手」
という中学生を本当に大勢みてきました。
関数が苦手な中学生の多くは,関数がなぜ便利なのかということを理解できていません。
本当は問題解決が「簡単」になるはずなのに・・・
例えば,表やグラフをかくことを面倒なことだと勘違いしている人は要注意です。
さて,
そんな関数ですが,ここ最近の小問集合での出題傾向から見てみましょう。

あらら,
ここ2年間は出題されてない!!!
なぜこんなことになっているのか。
その理由は,前回の方程式の記事の通りで,代わりに方程式の問題が出題されるようになったからなんですね。

とはいえ基本問題は頻出
確かにここ最近の出題がありませんでした。
それでも,頻出であることに間違いありません。
きちんと分析してどんな問題を対策しておくべきか確認しましょう!
そこで,
これまでに問われてきている内容を確認してみると・・・
確かに基本問題でありますが,いや~ほんと,嫌な感じ。
間違える人の多い内容をピンポイントでねらってきています。
この記事をしっかりと読んで,間違えやすい箇所を頭に叩き込んでください!
変化の割合を求める問題
まずは,
変化の割合を求めましょう
というよくある問題です。
「こんなの簡単」と思っていませんか?
それは一次関数のイメージかもしれません。
$$一次関数 y=ax+b$$であれば,確かに a と等しく一定ですからね。
そんなに難しくは感じません。
しかし
出題内容をみてください。
2回出題されていますが,どちらも $$関数 y=ax^2$$ で出題されています。
2次関数や反比例は変化の割合が一定ではありません!(だからグラフは曲線になりますね!)
きちんと変化の割合の公式を使って求める練習をしておきましょう!
$$変化の割合 = \frac {\ yの増加量}{ xの増加量 }$$
式を求める問題
次に,
xとyの関係を式で表しなさい
という問題です。
関数は式で定義されますので,式を求めることは基本中の基本。
与えられた値を代入して比例定数や傾き,切片を確実に求められるようにしておきましょう!
関数の式は
$$比例 y=ax$$
$$反比例 y = \frac {\ a }{ x }$$
$$一次関数 y=ax+b$$
$$関数 y=ax^2$$
です。それぞれすぐに思い出せるようにしておきたいですね。
特徴を選択する問題
次は,
正しいものを選びましょう
という問題です。
この問題は,それぞれの関数の特徴を正しく理解できているか?
ということが問われています。
例えば,
- 増減
- 正負
- 対応する値
- グラフの形状
- 平行移動
- 対称性
といったことに着目して,それぞれの関数の特徴を説明できるようにしておく必要があります。
一次関数(比例),反比例,2次関数に分けて,表にまとめておくと良いですね。
これからも関数の出題はない?
方程式の記事と同様に,関数もここ最近の傾向から言えば出題されないのでは?と思うかもしれません。
が!しかし!
小問集合で出題されている内容を理解できていないと,大問で出題される関数の問題を解くことはできません。
どれも確実に理解しておきたい内容です。
関数の基本をマスターすることで大問の正答率を上げる,そんな目標で小問集合の関数に取り組むことをおススメします!
また,
中学校の学習では割とないがしろにされがちな「変化の割合」は高校数学で重要になってきます。
変化の割合を調べることで,増減やグラフの形状を知ることができるという部分はきちんと押さえておきたいですね。

というわけで,
小問集合の”関数”領域の分析でした。
次回は”図形”領域の分析をしていきたいと思います。
中学生は忙しい!そんな中でも効率的に学習を進めていくには,正しく敵を知ることが大切です。
”図形”領域についても正しく情報をキャッチして,効率的・効果的な学習をしていきましょう!
それでは,
理想の進路実現に向けてファイト!
現在当塾では,
公式LINEにご登録いただいた方限定で学習の役に立つ以下のような豪華特典を10個以上無料で配布中です!
【電子書籍】元数学教師が伝授する中学数学の苦手克服「最初の教科書」完全版
【無限にできる!】最強の百マス計算シート!
【ひと目で確認!】グラフつき百マス計算記録シート!
【完全マスター】立式の基本「場面」と「図」 究極の20選!
【一撃理解】「あなたが秘めている本当の可能性」プレミアム動画 33分
【図解スライド】数学が苦手になる中学生の3つの真実 129枚
などなど
下記から公式LINEを友達登録していただいてキーワードの
やればできる
というひらがな6文字を打ち込んで是非お受け取りいただいてお使いください!
https://online.ogatatsuya.com/line/open/xDEEF9z80egM
<QRコードはコチラ🔽🔽>

それぞれの特典の使い方は
無料特典の1つである
【電子書籍】元数学教師が伝授する中学数学の苦手克服「最初の教科書」完全版
をぜひお読みください!
また
ここまで読んでいても
自分はどうせ変われないな
結局また分数でミスするんだろうな
もっとしっかり教えてもらいたいな
という気持ちが消えない場合は
完全オーダーメイドの個別相談を期間限定でやっております!
公式LINEに登録していただきお気軽にお申し込みください!
あなたにピッタリの具体的な対策をしっかりお伝えさせていただきます!

【完全オーダーメイド !】 『オンライン個別相談会』
これからも高校受験に向かって頑張る受験生たちのために情報発信していきます!
それではまた!
